|
|
|
|
Partie 1
Pour
se mettre en jambes...
Tout d'abord,
précisons que l'interface de Moonlight,
ainsi que les raccourcis clavier sont supposés connus des
utilisateurs. Ensuite, rappelons quelques notions élémentaires.
Un
volume, ou une surface, s'obtient à partir d'un profil que
l'on fait pivoter autour d'un axe (Revolution) ou que l'on
translate suivant un axe ou un chemin (Extrusion et Sweep).
Laissons de côté pour l'instant les volumes
prédéfinis que sont les Primitives, et les surfaces
complexes: Skin, Loft, Birail, Tube, Composite... Un profil sera
donc tracé, et il pourra l'être de plusieurs manières
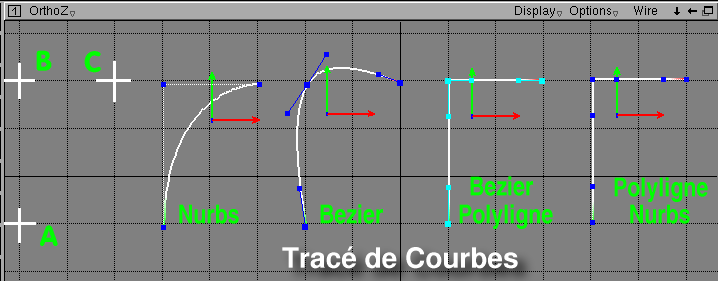
(voir figure Tracé de courbes
). Supposons que le profil soit défini par trois points A,
B et C. Nous disposons pour le dessiner de la courbe Nurbs, Bezier
et Bezier Polyligne, cette dernière pouvant être par
la suite convertie en Polyligne Nurbs. La figure parle
d'elle-même: avec les deux premières méthodes,
dans ce cas particulier, si l'on désigne les points A,B et
C, le résultat obtenu est sans doute loin de ce que l'on
était en droit d'attendre. Aussi est-ce pour cette raison
que dans la suite de l'exercice, il sera toujours fait appel à
la Bezier Polyligne. Celle-ci s'affine en déplaçant
(m+drag) les points de contrôle et les poignées des
tangentes.
Les surfaces
quant à elles, sont définies par une succession de
facettes. Si l'on génére un cylindre chanfreiné
par Révolution, à partir d'un profil Bezier
Polyligne, la surface obtenue est caractérisée par
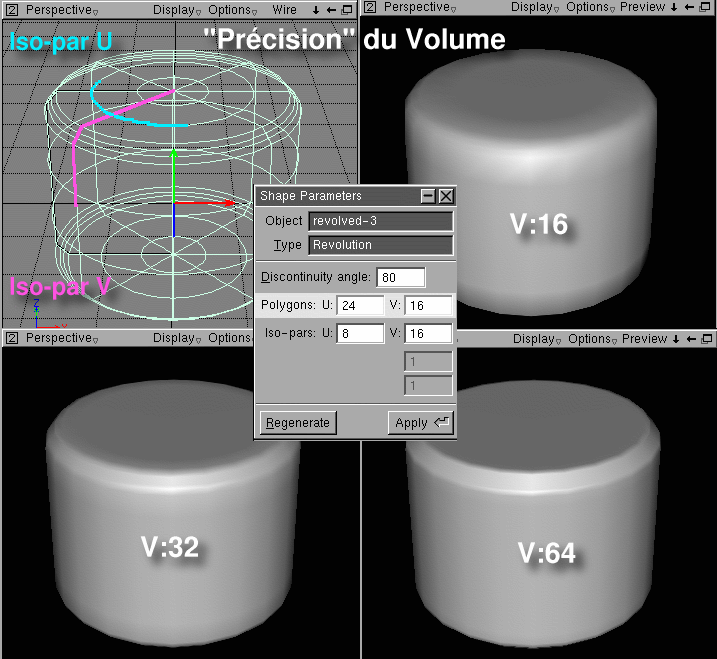
un nombre de polygones suivant U et V (voir
figure Précision du Volume ) attribués par
défaut. Une pré visualisation OpenGL de ce "volume",
montre que le chanfrein se présente comme un raccordement.
En augmentant la valeur V, la forme du "volume" devient
plus précise, et le chanfrein ressemble enfin à un
chanfrein. Evidemment, dans d'autres cas de figure, il eût
fallu augmenter la valeur U, ou U et V en même temps. Il
n'est ici question que du principe. Les Iso-par U (couleur cyan)
et V (couleur magenta) définissent le nombre de tracés
du "volume" en mode filaire, mais n'influent pas sur la
précision de celui-ci.
|