EXERCICE 1
| > | with(LinearAlgebra): |
| > | S := <<-1,0>|<0,1>>; |
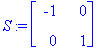
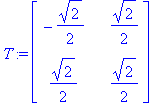
| > | T := (1/sqrt(2))*<<-1,1>|<1,1>>; |
| > | R := (S.T); |
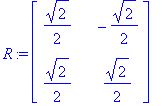
| > | seq(R^k,k=0..8); |
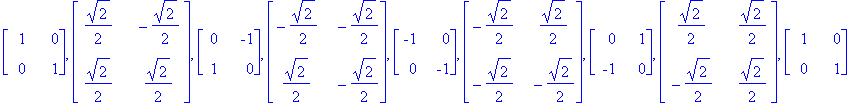
| > | S.R; |
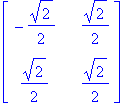
| > | Phi := M -> S.M; |
![]()
| > | liste := table([seq(R^k,k=0..7),seq(R^k.S,k=0..7)]); |
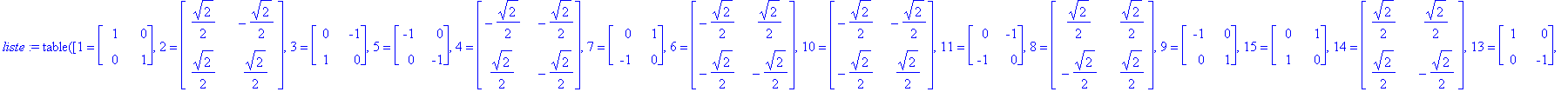
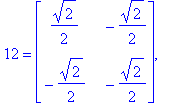
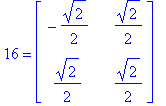
![]()
| > | sigma := proc(k) local j; for j from 1 to 16 do if Equal(Phi(liste[k]),liste[j]) then RETURN(j); fi; od; end: |
| > | sigma(1); |
![]()
| > | sigma := table([seq(sigma(k),k=1..16)]); |
![]()
| > | signature := product(product((sigma[j] - sigma[i])/(j-i),j=i+1..16),i=1..16); |
![]()
__________________________________________________________________________________________________________________________________________________________
EXERCICE 2
___________________________________________________________________________________________________________________________
| > | restart; |
| > | u := n -> evalf(product(1 + I/k^2, k = 1..n)); |
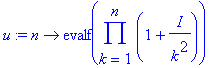
| > | v := n -> evalf(product(1 + 2*I/k, k = 1 .. n)); |
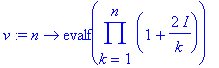
| > | P := (w,N) -> plot([seq([Re(w(j)),Im(w(j))],j = 1 .. N)]): |
| > | P(v,500); |
![[Maple Plot]](images/plancheCentrale216.gif)
| > | P(u,200); |
![[Maple Plot]](images/plancheCentrale217.gif)
| > | l := limit(u(n),n=infinity); |
![]()
| > | abs(l); |
![]()
| > | argument(l); |
![]()
| > | abs(u(6)); |
![]()
| > | argument(u(1000)); |
![]()
| > |
__________________________________________________________________________________________________________________________________________________________
EXERCICE 3
___________________________________________________________________________________________________________________________
| > | P := (n,x) -> product((1 + x/(2*k)) / (1 + x/(2*k - 1)), k = 1..n); |
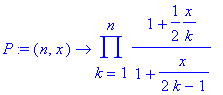
| > | assume(n,posint);simplify(limit(P(n,x),x=infinity)); |
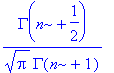
| > | plot([seq(P(n,x),n = 1..30)],x=0..20,thickness=[3,1$9]); |
![[Maple Plot]](images/plancheCentrale225.gif)
| > | p := x -> simplify(limit(P(n,x),n=infinity)); |
![]()
| > | assume(j,posint); |
| > | simplify(p(2*j)); |
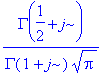
| > | seq(p(2*j),j=1..10); |
![]()
| > | pj := m -> ((2*m)!/((m!)^2*2^(2*m))); |
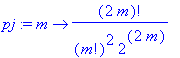
| > | seq(pj(j),j=1..10); |
![]()
| > | series(pj(j),j=infinity,2); |
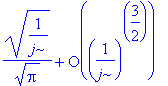
__________________________________________________________________________________________________________________________________________________________
EXERCICE 4
___________________________________________________________________________________________________________________________
| > | # question a |
| > | restart; |
| > | M1 := s -> [arcsinh(s), sqrt(1+s^2)]; |
![]()
| > | G := (M,s) -> map(z -> (1/s)*int(z,u = 0..s), M(u)); |
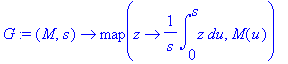
| > |
| > | Gamma := M -> plot([seq(M(0.1*s),s = 0..700)],color=blue): |
| > | Delta := M -> plot([seq(G(M,0.1*s),s = 0..1500)],color=red): |
| > | P := M -> plots[display](Gamma(M),Delta(M)); |
![]()
| > | P(M1); |
![[Maple Plot]](images/plancheCentrale235.gif)
| > | M2 := s -> [cos(s),sin(s)]: |
| > | P(M2); |
![[Maple Plot]](images/plancheCentrale236.gif)
| > | G(M2,s); |
![]()
| > | plots[display](Gamma(M2),Delta(M2),seq(plot([M2(s),G(M2,s)],color=wheat),s in [Pi/2,3*Pi/4,Pi])); |
![[Maple Plot]](images/plancheCentrale238.gif)
| > |
__________________________________________________________________________________________________________________________________________________________
EXERCICE 5
___________________________________________________________________________________________________________________________
| > | A := (X - 1)*(X - 2)*(X - 3): |
| > | B := X^3: |
| > | f := P -> rem(B*P,A,X); |
![]()
| > | P := a*X^2 + b*X + c; |
![]()
| > | solve([seq(coeff(f(P),X,k) = 0,k = 0..2)],[a,b,c]); |
![]()
| > | Q := collect(f(P) - lambda*P,X); |
![]()
| > | solve([seq(coeff(Q,X,k) = 0,k=0..2)],[a,b,c,lambda]); |
![]()
| > | with(LinearAlgebra): |
| > | mat := f -> Transpose(Matrix(3,3,[seq(seq(coeff(f(E),X,k),k=0..2),E in [1,X,X^2])])): |
| > | # Ou bien : mat := f -> <<seq(coeff(f(1),X,k),k=0..2)>|<seq(coeff(f(X),X,k),k=0..2)>|<seq(coeff(f(X^2),X,k),k=0..2)>>: |
| > | # ou bien : mat:= f -> Matrix(3,3,[seq(PolynomialTools[CoefficientVector](f(E),X), E in [1,X,X^2])]); |
| > | mat(f); |
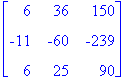
| > | Eigenvectors(mat(f)); |
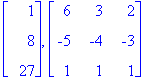
| > | ?lagrange; |
__________________________________________________________________________________________________________________________________________________________
EXERCICE 6
___________________________________________________________________________________________________________________________
| > | restart; |
| > | A := Matrix(6,6,(i,j) -> if j-i = 1 or (i,j) = (1,6) then 1 else 0 fi); |

| > | M := Matrix(6,6,(i,j) -> m[i,j]); |

| > | B := A.M - 2*M.A: |
| > | S := solve([seq(seq(B[i,j], j = 1..6),i=1..6)],[seq(seq(m[i,j], j = 1..6),i=1..6)]); |
![]()
![]()
| > | ?assign; |
| > | assign(S); |
| > | 4*M; |
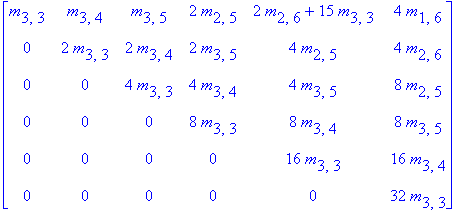
| > |
__________________________________________________________________________________________________________________________________________________________
EXERCICE 7
___________________________________________________________________________________________________________________________
| > | i1 := int(t^n*(1 - t)^m,t = 0..1); |
![]()
| > | convert(i1,factorial); |
![]()
| > | i2 := int(x^4*(1 - x)^4/(1 + x^2),x = 0..1); |
![]()
| > | 22/7 - (1/2)*int(x^4*(1 - x)^4,x = 0..1); |
![]()
| > | 22/7 - int(x^4*(1 - x)^4,x = 0..1); |
![]()
| > | 1979*2; |
![]()
| > | A := quo(x^4*(1 - x)^4,1 + x^2,x); |
![]()
| > | L := k -> int(A*(x*(1 - x))^(4*k), x = 0..1); |
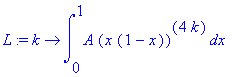
| > | L(0),L(1); |
![]()
| > | i3 := (1/4)*int(x^8*(1 - x)^8, x = 0..1); |
![]()
| > | L(0) - (1/4)*L(1) + (1/2)*i3; |
![]()
| > | L(0) - (1/4)*L(1) + i3; |
![]()
| > |